MANAGING WEATHER RISK DURING MAJOR SPORTING EVENTS:

THE USE OF WEATHER DERIVATIVES

S. S. Dawkins and H. Stern

 

Australian Bureau of Meteorology, Melbourne.

 

E-mail addresses: s.dawkins@bom.gov.au (S. S. Dawkins), h.stern@bom.gov.au (H. Stern).

 

ABSTRACT

Weather influences various activities, including most of the major outdoor sporting events across many countries. The revenue of major sporting events is influenced by, among other things, the ‘right’ kind of weather during the duration of a sporting event. This is because the ‘right’ kind of weather could influence the actual occurrence of a sporting event and also the number of people attending such an event. Hence, the uncertainty and the unpredictability of the ‘right’ kind of weather increase the revenue risk or revenue exposure, of the organisers of major sporting events. In the State of Victoria in Australia this is relevant in the case of major sporting events such as the Australian Open (Tennis), the Australian Formula 1 Grand Prix, the Australian Motorcycle Grand Prix, the Australian Rules Football Grand Final, and the Melbourne Cup (horse race).

 

This paper conducts a preliminary examination of the relationship between weather and revenue generated for a number of products associated with the Australian Open (Tennis) and the associated potential application of weather derivatives in ameliorating risks associated with the revenue generated.  Among the relationships found were that ground pass ticket sales purchased at the gate on the day of the event (as a proportion of total ground pass ticket sales) are negatively correlated with maximum temperature, that hat sales are positively correlated with both maximum temperature and sunshine hours, and that windcheater sales are negatively correlated with both sunshine hours and maximum temperature. No useful relationships were found in regard to the influence of rainfall due to the almost complete absence of rain during the period of available sales data.

 

It was shown that the application of weather derivatives may be a useful strategy in managing the weather-related risks associated with the generation of the Australian Open revenues.  For the purpose of illustration, the relationship between Per Capita Windcheater Sales and Sunshine Hours & Maximum Temperature was examined.  It was shown how, supposing that one wishes to compensate Windcheater marketers for poor sales on every occasion when the Per Capita sales are below 0.25%, to determine a "fair value" price of a weather derivative.

 

KEYWORDS

weather, risk, revenue, derivative, insurance, sport

 

INTRODUCTION

 

The application of weather derivatives, or weather insurance, has emerged in recent years as a tool to manage the revenue risks associated with businesses and other activities that are sensitive to the uncertainty and variation in weather conditions or the ‘weather risk’ (Geman, 1999, Stern 2001). In most situations, the term ‘weather risk’ relates to the exposure of earnings or revenues to the effect of meteorological phenomena such as unseasonal temperatures or rainfall. Weather derivatives are a form of financial instrument similar in nature to the commodity futures contracts and options, but their price is tied to some facet of the weather such as temperature, precipitation, wind, and heating (and cooling) degree-days (Dawkins & Stern, 2003; Stern & Dawkins, 2003, 2004). 

 

The weather insurance market, taken as a whole, is certainly growing.  In its 2003 survey, the Weather Risk Management Association (http://www.wrma.org) noted that, since its previous survey in 2002, there had been a near tripling of contracts transacted worldwide (to some 12,000 compared with 4,000 previously) although the notional value of contracts fell slightly ($US4.2 billion compared with $US4.3 billion previously). The total business generated over the past 6 years was $US15.8 billion and most transactions occur in the USA, but there are rapidly growing markets in Europe and Asia. Most contracts are related to protection against extremes in temperature, but there is a growing market in rain-related contracts.

 

Weather-linked securities may be used as channels for weather risk transfer and have prices that are linked to the historical weather in a region.  They provide returns related to weather observed in the region subsequent to their purchase. Therefore, they may be used to help businesses hedge against weather related risk.  They also may be used to help speculators monetise their view of likely weather patterns.

 

Emerging issues in the weather risk area include quality of weather and climate data, changes in the characteristics of observation sites, security of data collection processes, privatisation of weather forecasting services, the value of data, and the issue of climate change.

 

The Weather Risk Management Association states that “nearly one-third of the USA economy or $3.5 trillion is at risk due to weather”, and they are optimistic about world wide growth in the weather derivatives market. With respect to the potential development of the weather derivative market in Australia, a survey in 2002 identified 15 contracts valued at $A25 million.  The Australian market is considered relatively small and the use of weather derivatives is developing slowly.  Further growth in the area of temperature derivatives for (energy) utilities and in rainfall for hydroelectricity power and agribusiness was foreshadowed.  The practice is to undertake contract settlement on the basis of the official observations, partially settling contracts almost immediately, and then awaiting confirmation (following quality control procedures) for final settlement.  The Weather Risk Management Association designates an official authority in each country from which meteorological data can be obtained, typically the national meteorological service.  Employees of the observing authority are not permitted to trade in weather contracts.

 

METHODS

 

The purpose of this work is to conduct a preliminary examination of the relationships between several Australian Open (Tennis) products and the associated weather conditions.  The products of interest are:

Once these relationships are established, they may be utilised by marketers to predict profits on a day-to-day basis (determined using the official weather forecasts). This could allow the risk to be minimised using a weather derivative. An example of such an application will be shown.

 

Data

Weather information (2001-2004) was provided by the Australian Bureau of Meteorology. Maximum daily temperature data and daily rainfall totals were measured at the Melbourne Regional Office site (World Meteorological Organization (WMO) no. 94868), whilst daily sunshine hours data was measured at the Melbourne Airport site (WMO no. 94866). Information on ground pass ticket sales (2001-2004) and merchandise sales (2004) from the Australian Open was provided by Tennis Australia. Data from days 1-8 of the tournament were chosen to be used for this study. After day 8, scheduling on the outside courts reduces significantly. This ensured the validity of any relationships found.

 

The ground pass ticket sales information that were of particular interest were the walkup sales. The raw walkup ground pass sales totals were expressed as a proportion of the total ground pass ticket sales for analysis. Merchandise data was expressed as sales per total number of people attending the Open on a particular day (per capita = no. of sales/total attendance).

 

RESULTS

 

The weather information was plotted against the sales information (both ground pass ticket and merchandise) (Figures 1-2).  Although the data set was not large, there were some clear relationships evident. After conducting regression analysis on the data, a series of relationships were derived, and these, and their significance using the t-test, are presented in Table 1.

 

Firstly, windcheater sales (per capita) showed a negative correlation with both sunshine hours and maximum temperature data (Figures 1-2). It was expected that the sales of such an item would be negatively correlated with both maximum temperature and sunshine hours. The relationship of windcheater sales and sunshine hours proved to be significant at the 98% level (t-test), whereas the relationship between maximum temperature and windcheater sales was not as strong. The fact that sales increased when conditions were cooler and less sunny is not surprising. Also, as the sun can ameliorate the impact of lower temperatures, the relationship is not as strong with maximum temperature. People tend to feel more comfortable on a 20°C sunny day than they would on a 20°C overcast day. The day of most sales (per capita) had zero sunshine hours and the lowest maximum temperature recorded during the period of data.

 

Table 1. Significance of relationships

 

Significance of relationship

Maximum Temperature (T)

Total Sunshine Hours (S)

Relationship Equation

Windcheater Sales (W)

56%

98%

W = 0.0197-0.000989*S-0.000198*T

Hat Sales (H)

67%

70%

H=0.0148+0.000354*S+0.000269*T

Walkup Gate sales (G)

51%

7%

G = +60.189-0.518*T+0.0325*S

 

Secondly, hat sales (per capita) were positively correlated with both sunshine hours (R squared=+0.25) and maximum temperature (R squared=+0.23).  The sun necessitates people to reduce the risk of sunburn and skin cancer by wearing a hat. High temperatures reminds people of the sun – as it does not need to be particularly sunny for people to get badly burnt, especially if they are sitting outside for prolonged periods. From the available data set, the lowest level of hat sales also corresponded to the day with no sunshine and the lowest maximum temperature.

 

Thirdly, walkup gate sales (as a proportion of total ground pass ticket sales) were negatively correlated to the maximum temperature. This relationship was highly significant (>95%)(Table 1). This strong relationship may be, in part, related to the "Australian Open extreme heat policy". With this in mind, should a very hot day (~38°C/100°F) be anticipated, the public may well be discouraged from attending; also, the prospect of sitting for long periods in high temperatures may discourage people from attending the Australian Open. The relationship between gate ground pass sales and sunshine hours was not significant.

 

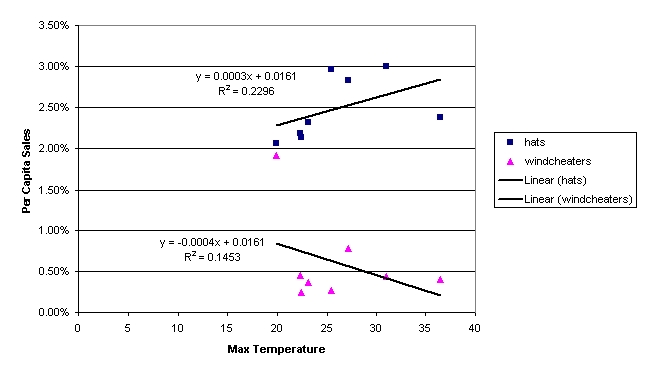
Figure 1: Merchandise sales vs. Maximum Temperature


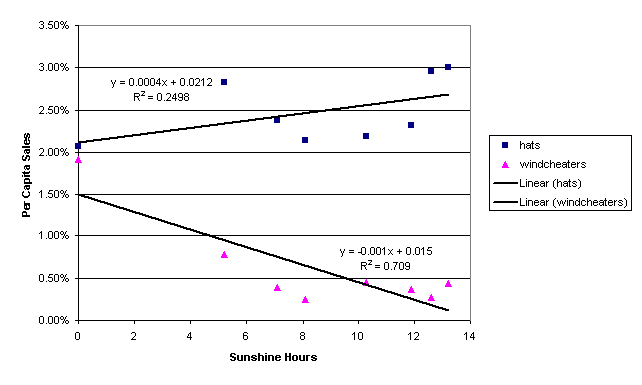
Figure 2: Merchandise sales vs. Sunshine Hours

 

Application

How this approach might be used in application is now addressed. For the purpose of illustration, the relationship between Per Capita Windcheater Sales and Sunshine Hours & Maximum Temperature is examined, namely:

Per Capita Windcheater Sales = +0.0197-0.000989(Sunshine Hours)-0.000198(Max Temp) (R squared=0.74; n=8)

 

In general when estimating the demand for a service, you look at the price variable. In this case we have not taken into account the price variable.

 

The relationship has been developed using data from the Australian Open 2004 and will now be discussed.  Suppose that one wishes to compensate Windcheater marketers for poor sales on every occasion when the Per Capita sales are below 0.25%.  Also suppose that, when the Per Capita sales are below 0.25%, $100 compensation (an amount that we have chosen quite arbitrarily) is attributable for every 0.01% below 0.25%. This is a synthetic Put Option with a "strike" of 0.25%, that is, a pay-off occurs whenever the Per Capita sales are below 0.25% on any particular day.

 

Applying the equation to 24 days of data from the earlier years (2001-2003), there were only 3 days when the Per Capita sales would have been below the "strike".  For example, for Day-5 2001, the Per Capita sales predicted, using the relationship derived, were 0.15% - this Per Capita value is 0.10% below the "strike", leading to a payout of $1000; for Day-6 2002 (0.09% - payout $1600); and, for Day-7 2003 (0.21% - payout $400).  This then leads to a total payout of $3,000 over the 24 days.  This then suggests a "fair-value" price of the option of $125 per day ($3000/24 days).

 

DISCUSSION

 

This paper has presented the results of a preliminary examination of the relationship between weather and revenue generated for a number of products associated with the Australian Open (Tennis) and the associated potential application of weather derivatives in ameliorating risks associated with the revenue generated.  Among the relationships found were:

-         Ground pass ticket sales on the day of the event (as a proportion of total ground pass ticket sales) are negatively correlated with maximum temperature.

-         Per capita hat sales are positively correlated with both maximum temperature and sunshine hours.

-         Per capita windcheater sales are negatively correlated with both sunshine hours and maximum temperature.

No useful relationships were found in regard to the influence of rainfall due to lack of rain during the period of available sales data.

A "fair value" price of a synthetic put option with a strike of 0.25% was determined to be $125 (this may be used to compensate Windcheater marketers for poor sales on every occasion when the Per Capita sales are below 0.25%).

 

CONCLUSION

 

We have shown that there are relationships between the sales of various products and various weather parameters associated with the Australian Open. Using a simple illustrative example, we highlighted the potential of weather derivatives to guarantee the income associated with these products.  Future work may involve the application of some thermal comfort index.

 

ACKNOWLEDGEMENTS

The authors wish to gratefully acknowledge Tennis Australia's Cameron Pearson and Sarah Clements, for their advice, Dean Collins, Don Gunasekera, and Andrew Watkins for their helpful comments, and specifically Tennis Australia, for making their data available.

 

REFERENCES

Dawkins, S. S. and Stern, H. 2003 Cashing in on the weather: how agriculture might protect against adverse seasons using weather derivatives, Australia New Zealand Climate Forum: Climate Serving Agriculture, Palmerston North, New Zealand, 19-21 Mar., 2003.

Geman, H. 1999 Insurance and weather derivatives. From exotic options to exotic underlyings. Risk Books, 213 pp.

Stern, H. 2001 The application of weather derivatives to mitigate the financial risk of climate variability and extreme weather events, Aust. Meteor. Mag., Vol 50, September 2001.

Stern, H. and Dawkins, S. S. 2004 Weather derivatives as a vehicle to realise the skill of seasonal forecasts, 15th Conference on Global Change and Climate Variations & 14th Conference on Applied Climatology, Seattle, Washington, USA 11-15 Jan., 2004.

Stern, H. and Dawkins, S. S. 2003 Pricing a financial instrument to guarantee the accuracy of a weather forecast, Third Conference on Artificial Intelligence Applications to Environmental Science, Long Beach, California, USA 9-13 Feb., 2003. Refer also (for a report on the presentation) to At the Annual Meeting ... Pricing forecast guarantees. Bulletin of the American Meteorological Society, March 2003, 84:325-326.